分类问题
7-1 过拟合
过拟合是指模型过度拟合训练数据,而导致无法泛化去预测新的数据,即在训练数据上模型表现非常好,但在测试数据中表现很差。
一般在特征过多,训练数据较少的时候会出现过度拟合的现象。解决过度拟合的办法一般是:
- 减少特征数 手动选择特征 使用模型选择算法
- 正则化 保留所有的特征,但是减少特征的数量级 在所有特征都能对结果产生一点点影响时非常有用
7-2 正则化代价函数
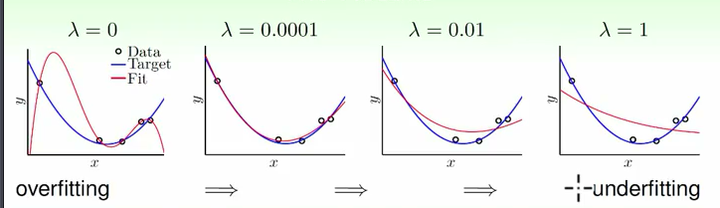
正如上节提到的,为了避免过多特征参数造成过拟合,可以对代价函数正则化。正则化的核心思想可以参考上图,我们给代价函数加上\(1000\theta_3^2\)和\(1000\theta_4^2\),这样一来,\(\theta_3\)和\(\theta_4\)只要发生微小的变化都会导致代价函数发生很大的变化,换句话说就是,给\(\theta_3\)和\(\theta_4\)加上一个比较大的惩罚,从而让它们接近于0。
由于并不知道应该选哪一个参数进行惩罚,于是给每一个参数都乘以一个\(\lambda\),代价函数变成如下的形式:

代价函数实现正则化后,训练就倾向于得到平滑的低维曲线:
为什么正则化后的代价函数会起作用?
过拟合的时候,拟合函数的系数往往非常大,而正则化是通过约束参数的范数使其不要太大,所以可以在一定程度上减少过拟合情况。
如下图所示,过拟合,就是拟合函数需要顾忌每一个点,最终形成的拟合函数波动很大。在某些很小的区间里,函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值(绝对值)非常大,由于自变量值可大可小,所以只有系数足够大时,才会导致导数值很大。

过拟合的产生主要有四个因素:
- 数据量小,低于PAC规定的最小数据量。
- 数据噪音大,很多乱七八糟的点干扰了学习的过程,重点完全跑偏了。
- 模型任务本身很复杂,这种情况下不管怎么搞都效果不好,或多或少会过拟合。
- 假设空间H太大,比如说从二项式、三项式甚至到1024项式都有,最后我们选择的最优模型必然是高次项的模型,这种情况下必然过拟合。
以上4个情况就会造成过拟合,其中1可以通过增大数据集解决,2可以通过数据清洗和预处理解决,3这个东西我感觉是听天由命的,只剩下4是我们可以做但是又比较复杂的。
如果的假设空间里有二次多项式模型、三次多项式模型等等,那么如何解决假设空间太大的问题呢?
先看一下二次多项式和十次多项式的区别——
二次多项式:\(w_0+w_1x+w_2x^2\)
十次多项式:\(w_0+w_1x+w_2x^2+...+w_{10}x^{10}\)
下图可以看出来十次项的身材很妖,虽然可以拟合训练集全部数据,但是严重过拟合。我们尝试把十次项出现的机会打压一下。
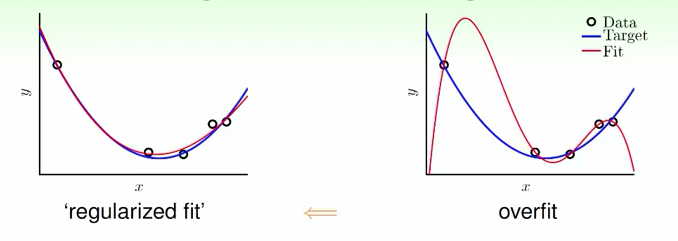
其实只要让后面的w系数全等于零,那么二次多项式和十次多项式本质上是一样的,这样子就客观上把假设空间缩小了,这里就是正则化的过程。
正则化的英文是Regularization,其词根是regulate也就是“监管”的意思,所以这里我们监管好模型的参数就好。
第一种做法
可以加上一个约束:\(w_3=w_4=...=w_{10}=0\),这样子全部的十项式都变成二项式了,这个正则化太矫枉过正了,完全抛弃了高次项存在的意义。
第二种做法
我们退步一点,只规定某些参数为零,数量规定但是随机选择。\(\sum^{10}_q[w_q=0]>8\) 这个约束规定了8个以上参数必须为零(可以是第一个也可以是第二个)。但是这种离散的、稀疏的参数选择条件是NP-hard的,不具备大规模使用的能力。
第三种做法
在刚才那个过程上再做退步,只约束参数的总值,有\(\sum^{10}_{q=0}w_q^2<C\) 。但是这种约束取决于常数C的值,如果C非常大的话实际上是没有意义的。C具体怎么手动选择也是问题。
第四种做法
把C融合到目标函数中,原目标函数是预测值和整数值的函数,我们希望它越小越好\(\sum[y-wx]^2\)。这个时候我们把正则化时要用的参数加到目标函数中,变成\(\sum[y-wx]^2+\frac{\lambda}{2}w^2\),我们希望这个新的方程最小化。
最后我得出的这个方程非常的眼熟,其实这就是统计中的Ridge回归。如果把正则化部分写成二范数就有\(\Vert w\Vert^2_2\),这是不是更眼熟了……如果写成\(\Vert w \Vert_1\),那上面就变成Lasso回归了。其中\(\lambda\) 是自己定义的,不同的值有不同的正则化效果,太小了等于没有作用——